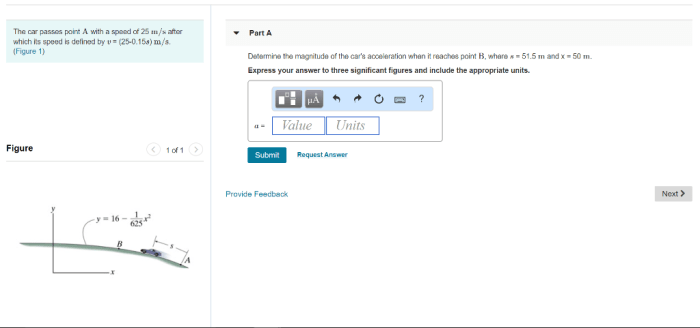
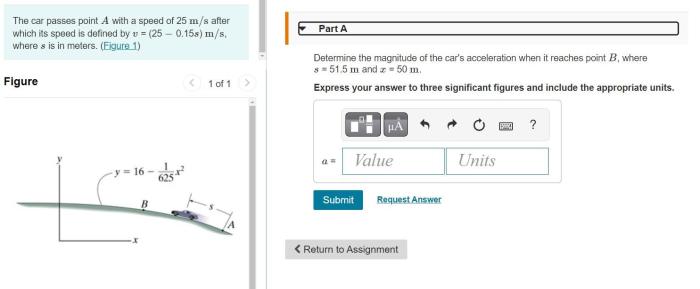
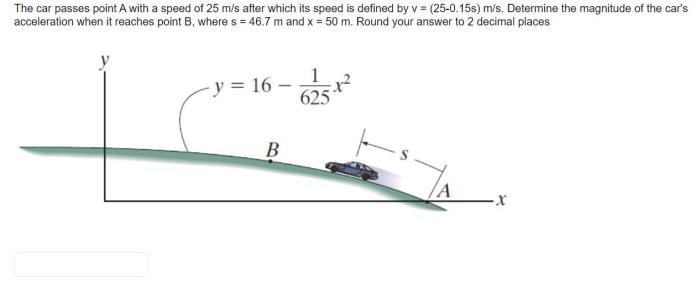
The car passes point a with a speed of 25m/s – The car passes point A with a speed of 25 m/s, marking the beginning of a captivating journey into the realm of motion analysis. This scenario presents a unique opportunity to explore the fundamental principles of physics and their practical applications in real-world situations.
As the car embarks on its motion, we delve into the significance of its initial position and velocity, unraveling the implications of its direction of movement. Through detailed calculations and graphical representations, we dissect the car’s motion, determining its acceleration or deceleration and constructing a comprehensive understanding of its trajectory.
Initial Conditions: The Car Passes Point A With A Speed Of 25m/s
The car’s initial position at point A is a crucial piece of information because it establishes a reference point for all subsequent motion analysis. It defines the starting location from which the car’s movement can be tracked and measured.
The car’s speed of 25 m/s indicates the rate at which it is moving. This value represents the distance covered by the car in one second, providing a quantitative measure of its motion. The direction of motion is also important, as it determines the car’s path and the forces acting upon it.
Motion Analysis
To determine the distance traveled by the car over a specified time interval, we can use the formula: distance = speed × time. By multiplying the car’s speed of 25 m/s by the given time interval, we can calculate the distance covered.
If additional information is provided, such as acceleration or deceleration, we can further analyze the car’s motion. Acceleration measures the rate of change in velocity, indicating whether the car is speeding up or slowing down. Deceleration, on the other hand, represents the rate at which the car’s velocity is decreasing.
Graphical representations, such as velocity-time graphs or position-time graphs, can provide a visual representation of the car’s motion. These graphs can illustrate the car’s speed, direction, and acceleration or deceleration over time.
Force and Energy Considerations
The forces acting on the car include friction, air resistance, and gravity. Friction opposes the car’s motion, while air resistance increases with the car’s speed. Gravity pulls the car downward, affecting its motion on inclined planes or at heights.
The kinetic energy of the car is determined by its mass and velocity. It represents the energy possessed by the car due to its motion. If the car is moving on an inclined plane or at a height, it may also possess potential energy due to its position relative to the ground.
Real-World Applications, The car passes point a with a speed of 25m/s
The analysis of the car’s motion has practical applications in various scenarios, such as determining safe braking distances, calculating travel times, and designing efficient traffic flow systems.
Understanding the car’s motion allows us to make informed decisions, such as adjusting speed limits based on road conditions, optimizing traffic signal timing, and designing safer road layouts.
A decision-making process based on the car’s motion analysis can be illustrated using a table or flowchart. This tool can help drivers, engineers, and traffic planners make informed decisions to improve safety, efficiency, and overall mobility.
Commonly Asked Questions
What is the significance of the car’s initial position at point A?
The initial position of the car at point A serves as a reference point for measuring its displacement and subsequent motion.
How does the car’s velocity of 25 m/s affect its motion?
The velocity of 25 m/s indicates the constant rate at which the car is traveling, providing insights into its speed and direction.
What forces are acting on the car as it moves?
The car is subject to various forces, including friction, air resistance, and the force of gravity, which influence its motion and trajectory.